자 그동안 저희는 머신러닝에 대해서
학습을 해보았습니다.
이제 이번 강의부터 본격적으로 딥러닝에 대해서
다루기 시작합니다.
딥러닝에 대한 정리들을 한번 시작해보겠습니다.
역시나 위키독스를 참고하여 정리해보도록 하겠습니다.
그 첫 시작은 DNN입니다.
학습 목표
퍼셉트론(Perceptron)에 대해 알아본다.
다중 퍼셉트론(Multi Layer Perceptron) 에 대해 알아본다.
핵심 키워드
퍼셉트론(Perceptron)
선형 분류기(Linear Classifier)
AND, OR, XOR 게이트
다중 퍼셉트론(Multi Layer Perceptron)
오차역전파(Backpropagation)
1. 퍼셉트론(Perceptron)
퍼셉트론은 우리의 신경 세포에서 착안하여 설계한 인공 신경망으로 다수의 입력으로부터 하나의 결과를 출력하는 알고리즘입니다.


처음 퍼셉트론은 아래와 같이 Linear 한 문제들을 해결하기 위해 제안되었습니다.

퍼셉트론이 개발되면서 사람들은 이를 이용해서 AND, OR 문제를 풀 수 있게 되었습니다. 이는 인공지능 분야에서 매우 획기적인 일이었습니다.


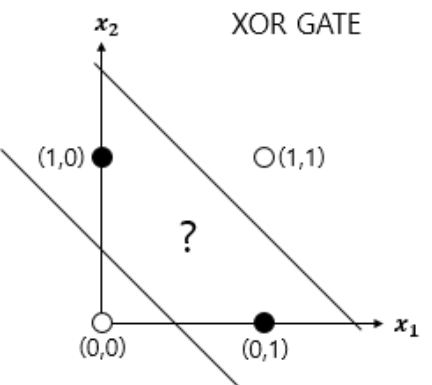
하지만 문제가 생겼습니다. 이렇게 LInear 한 방법으로는 맨 오른쪽 사진과 같이 도저히 XOR과 같은 문제를 해결할 수 없는 것이지요. 이러한 문제를 해결하기 위해서는 다중 퍼셉트론(MultiLayer Perceptron, MLP)의 필요성이 제기됩니다. 말 그대로 여러 개의 층을 두는 것이지요. 여러개의 은닉층을 둠으로써 여러개의 가중치를 갖게 되고 이를 통해 XOR문제와 같이 복잡한 문제를 풀 수 있게 됩니다. 여기서 은닉층이 2개 이상인 신경망을 다른 말로 심층 신경망(Deep Neural Network, DNN)이라고 부릅니다.

하지만 여기서 문제가 발생하게 됩니다. 바로 여러 개의 가중치를 자동으로 학습시킬 방법이 없는 겁니다. 그러면서 AI 분야는 암흑기에 빠지게 됩니다. 이러한 암흑기 속에서 AI를 구출해준 알고리즘이 바로 Backpropagation입니다.
2. Backpropagation
이제 딥러닝에서 매우 매우 매우!!! 중요한 backpropagation에 대해서 배워보도록 하겠습니다. backpropagation이란 쉽게 생각하면 각 입력값, 노드들이 최종 출력 값에 미치는 영향이라고 생각하시면 됩니다. 이렇게 말로만 설명하면 이해가 되지 않기 때문에 CS231n 강의에 나온 예제를 바탕으로 설명드리도록 하겠습니다.

위에 사진을 보면 각 노드마다 두 개의 숫자가 적혀 있습니다. 위에 있는 숫자는 우리가 흔히 아는 사칙연산을 통해 구해진 forward pass 값입니다. 직관적으로 쉽게 이해하실 수 있을 겁니다. 반면 아래에 있는 숫자는 backpropagation이라는 방법을 통해 구하게 될 backward pass입니다. 이 backward pass의 값이 바로 해당 노드가 최종 출력 값에 미치는 영향입니다. 어떤 값이 어떤 값에 미치는 영향을 구할 때는 미분이라는 개념을 통해 구하게 됩니다. 즉 x가 f에 미치는 영향은 ∂f/∂x, y가 f에 미치는 영향은 ∂f/∂y와 같이 표현할 수 있습니다. 그럼 우선 backpropagation에 필요한 몇 가지 미분 값을 먼저 구하겠습니다.
∂f / ∂q = z , ∂f / ∂z = q
∂q / ∂x = 1 , ∂q / ∂y = 1
이렇게 간단한 미분 값을 구했으면 이제 backward pass를 본격적으로 구해보도록 하겠습니다.
먼저 q가 f에 미치는 영향은 위에서 구한 것과 같이 z=-4입니다. 즉, q를 1만큼 증가하였을 때 f는 -4배 증가합니다. 같은 방법으로 z가 f에 미치는 영향은 3입니다.
이제 x가 f 에 미치는 영향을 구해보도록 하겠습니다. 이를 구하기 위해서는 Chain Rule을 적용하면 아주 쉽게 구할 ㅅ 있습니다. x가 f에 미치는 영향을 아래와 같이 나타낼 수 있습니다.
∂f / ∂x = ∂f / ∂q * ∂q / ∂x
위의 식과 앞에서 구한 미분 값들을 통해 x의 backward pass를 구하면 -4 ×1=-4 임을 구할 수 있습니다. 이와 동일한 방법으로 y의 backward pass를 구하면 동일하게 -4가 됩니다.
동일한 방법으로 미분만 할 줄 안다면 그 어떠한 복잡한 식도 단계별로만 나눈다면 backward pass를 구할 수 있습니다.


위의 시그모이드 식을 주어진 미분 값을 이용해서 아래와 같이 backward pass를 구해보시기 바랍니다.

3. XOR 다층 퍼셉트론
이제 아래와 같이 3개의 은닉층을 가진 다층 퍼셉트론을 이용해서 XOR 문제를 실습을 통해 해결해보도록 하겠습니다.

import torch
import torch.nn as nn
device = 'cuda' if torch.cuda.is_available() else 'cpu' # gpu가 사용가능 하다면 gpu를, 불가능하다면 cpu를 사용
# 랜덤시드 고정
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# data
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device) # .to()연산을 실시하고자 하는 device
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)이제 본격적으로 입력층, 3개의 은닉층, 출력층을 가진 모델을 생성하도록 하겠습니다.
# model
model=nn.Sequential(
nn.Linear(2,10,bias=True),
nn.Sigmoid(),
nn.Linear(10,10,bias=True),
nn.Sigmoid(),
nn.Linear(10,10,bias=True),
nn.Sigmoid(),
nn.Linear(10,1,bias=True),
nn.Sigmoid()
).to(device)비용 함수로는 이진 분류에서 사용하는 크로스 엔트로피 함수를 사용하고, SGD를 통해 optimizer을 진행합니다.
criterion = torch.nn.BCELoss().to(device) # 비용함수
optimizer = torch.optim.SGD(model.parameters(), lr=1)총 10001번의 epoch를 수행하고 각 epoch마다 backpropagation을 수행합니다.
for epoch in range(10001):
optimizer.zero_grad()
# forward 연산
hypothesis = model(X)
# 비용 함수
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
if epoch % 100 == 0:
print(epoch, cost.item())# 학습결과
0 0.6948983669281006
100 0.693155825138092
200 0.6931535005569458
300 0.6931513547897339
400 0.693149209022522
500 0.6931473016738892
600 0.6931453943252563
700 0.6931434273719788
...
5400 0.009703822433948517
5500 0.005025677848607302
5600 0.0032926425337791443학습 결과를 보면 매우 잘 학습이 진행되었음을 알 수 있습니다.
이번 시간에는 딥러닝에서 가장 기본적인
퍼셉트론과 이를 여러 개의 층을 가진
다층 퍼셉트론,
다층 퍼셉트론을 학습시키기 위해
가장 핵심적인 backpropagation에 대해서
배워보았습니다.
다음 시간에는 딥러닝에 사용되는 비활성 함수, Weight 초기화, batch nomalization 등을
배워보도록 하겠습니다!

'모두를 위한 딥런닝 by PyTorch' 카테고리의 다른 글
| Lab-8 CNN (0) | 2021.09.06 |
|---|---|
| Lab 07-2 DNN (0) | 2021.09.05 |
| Lab-06 Softmax Classification (0) | 2021.08.14 |
| Lab-05 Logistic Regression (0) | 2021.08.12 |
| Lab-04-2 Minibatch Gradient Descent (0) | 2021.08.09 |



